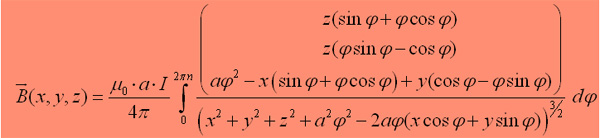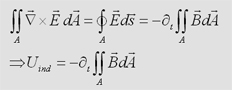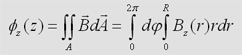Theoretische Betrachtungen zur angewandten Elektrodynamik
Berechnung der Magnetfelder von Spulen
Feldverteilung einer Flachspule
1.
Das Biot-Savart-Gesetz
Felder von beliebigen Spulenanordnungen lassen sich nur unter sehr einfachen
Randbedingungen analytisch berechnen. In gewöhnlicher Literatur zur
Experimentalphysik oder Theoretischer Physik (z.B. Demtröder, Pohl,
etc.) gibt es meist die Aufgabe das Magnetfeld entlang der Mittelachse
durch eine Ringspule zu berechnen. Solche Problemstellungen können
mit dem Biot-Savart-Gestetzt durch Integration über alle Volumenelemente
bzw. Linienelemente der jeweiligen Spule analytisch berechnet werden.
Möchte man dagegen kompliziertere Spulenanordnungen (was scheinbar
einfache Anordungen, die kein Gerade sind, auf jeden Fall erfüllen)
muss man das Biot-Savart-Gesetz in numerischen
Berechnungen verwenden.
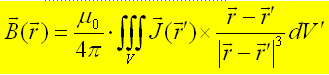 (1.1) (1.1) |
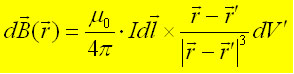 (1.2) (1.2) |
| Biotsavartgesetz bei bekanntem Stromdichtevektorfeld | Partielle Flussdichte bei homogener Stromdichteverteilung |
Wie aus den beiden Formeln ersichtlich, trägt jeder Stromdichtevektor in einem Leiterelement zur Bildung der Magnetischen Flussdichtevektors an einem bestimmten Punkt r bei. In anderen Worten: Die Summe aller möglicher Kreuzprodukte der Stromdichte J mit den "gewichteten Absatndvektoren" bildet im Grenzfall bei unendlich viel Summationen den magnetischen Flussdichtevektor am Punkt r.
2. Die Spulenfunktion
| Die Flachspule hat
die Form einer archimedischen Spirale. Der Ortsvektor r´(f)
läuft je nach Winkel f die Spirale ab. Mathematisch gilt also: |
|

|
|
Die
Funktion der archime-dischen Spirale mit Windungsabstand
d lautet: |
|
3. Der Abstandvektor Als Abstandvektor
R* soll der Verbindungsvektor zwischen r und r'
bezeichnet werden: |
|
|
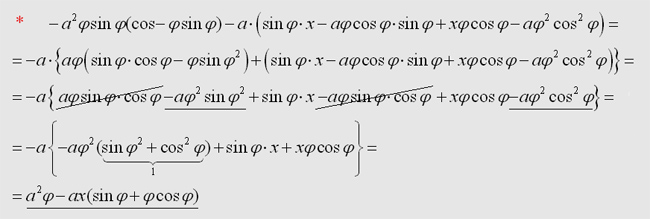 |
||
5. Berechnung des Abstandvektorbetrags |
6. Darstellung des Integrals |
|
|
|
 |
|
|
Das
Magnetfeld einer Flachspule kann entweder mit der Formel oben berechnet
werden und je nach Anwendung von einer Rotationssymetrie um die
z-Achse ausgegangen werden. Eine genaue Berechnung ist nur mit der
Formel rechts möglich, die sich mit einem allgemeinen Ansatz
ohne die Randbedingung y=0 herleiten lässt. |
|
|
| Numerische Berechnungen |
||
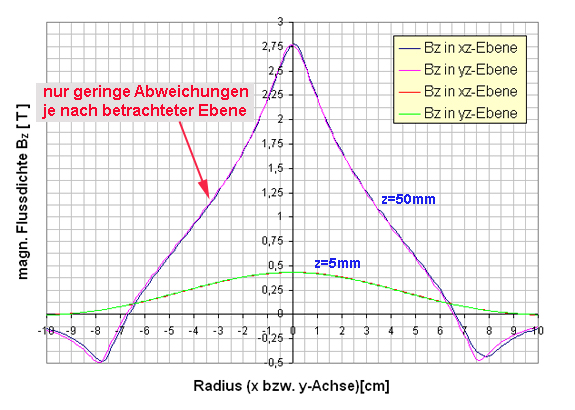
| Für Experimente, deren Funktion auf Induktion mit Flachspulen basiert, ist es hilfreich die Feldverteilung in Bz-Richtung genau zu analysieren. Bei weiteren numerischen Berechnungen ist es zunächst sinnvoll zu entscheiden, inwieweit bei der jeweiligen Spule von einer Rotationssymetrie um die z-Achse ausgegangen werden werden kann. Für einen ersten Eindruck kann man die Bz-Verteilung in der xz-Ebene mit der in der yz-Ebene vergleichen. Folgende
Diagramme zeigen die Feldverteilung für die im Projekt Metallverformung
durch Kurzpulsmagnetfelder verwendete Flachspule
FL1 bei einer Strombelastung von I=10kA. |
 |
|
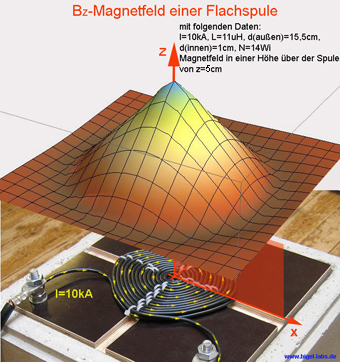 |
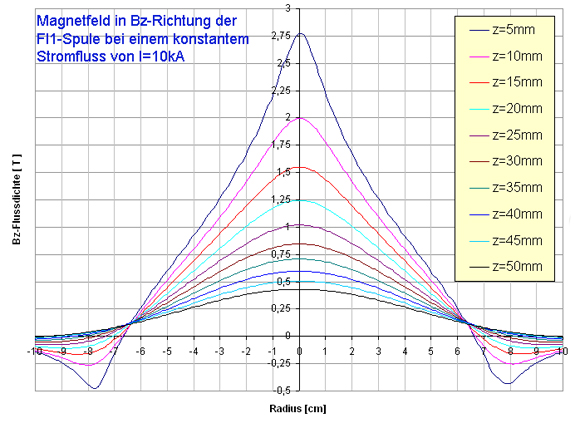
numerisch berechnete Bz-Verteilung der Fl1-Spule mit Simpson-Algorithmus in den Höhen z über der Spule bei einer konstanten Stromstärke von 10.000 A. | |
 |
||
| Je
nach betrachteter Höhe z über der Spule ergibt sich eine
andere Flussdichteverteilung in Bz-Richtung. Besonders interessant
ist der gemeinsame Schnittpunkt der Funktionen bei einem Radius
von ca. 6,4cm im Diagramm rechts. |
||
| Magnetischer Fluss einer Flachspule |
||
| Aus
der Maxwellgleichung |
 |
|
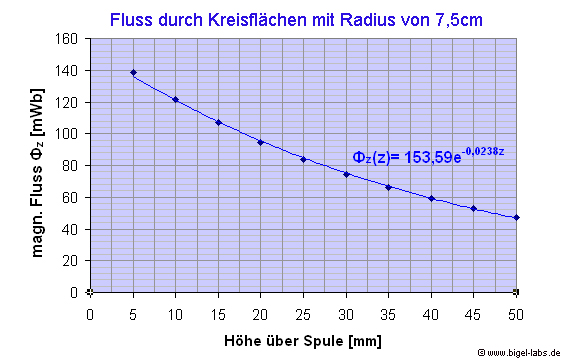
| Magnetischer
Fluss durch "virtuell erdachte Kreisringe" mit Radius
7,5cm über der Spule in Höhe z |
||
| Für
Versuche bei denen Metalle während den Magnetpulsen von der Spule
weg beschleunigt werden ist es von Bedeutung, eine quantitative Vorstellung
davon zu bekommen, bei welchem Abstand wieviel Prozent des ursprünglichen
Magnetischen Flusses noch das Metallblech durchdringen. Die magnetischen Flüsse (Einheit 1Weber=1Tesla*m^2) können nach der numerischen Berechnung in verschiedenen Höhen z über der Spule in einem Diagramm eingetragen und die Punkte durch eine e-Funktion interploliert werden. Somit steht z.B. für Simulationen eine Funktion Phi(z) zur Verfügung, um auch bei variablen Kreisflächenpositionen den magnetischen Fluss durch diese Flächen berechnen zu können. |
 |
|
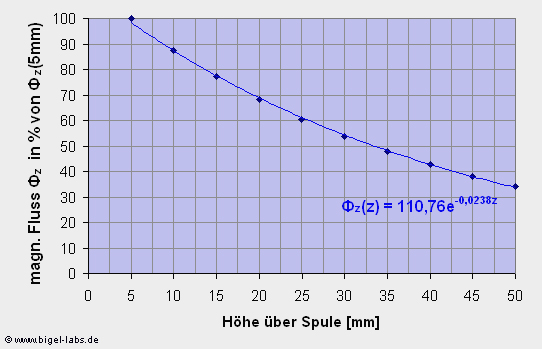
Magnetischer Fluss durch "virtuell erdachte Kreisringe" mit Radius 7,5cm über der Spule in Höhe z als prozentualer Anteil des Flusses bei z=5mm. |
||
|
|
||
letzte Änderung 19.10.2009, 3.11.2010

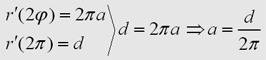
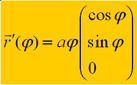 Bewegungsvektor
für archimedische
Spirale
Bewegungsvektor
für archimedische
Spirale 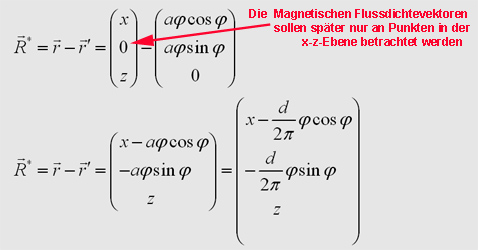
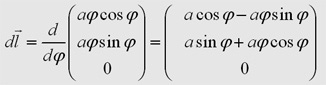
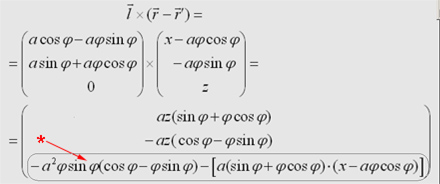
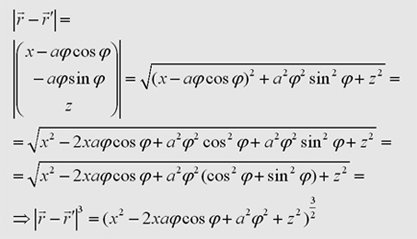 Die
einzelnen Komponenten des Integrals können nach der hergeleiteten
Formel nur in der x-z-Ebene berechnet werden.
Die
einzelnen Komponenten des Integrals können nach der hergeleiteten
Formel nur in der x-z-Ebene berechnet werden.