Physics

Rope Swing- Climbing Rope Tests

Climbing Rope Knot Tests
experiments to understand the break behavior of different knots

1. Mechanical Strenght of Knots in the Literature 2. Knot Strenght Tests with old Climbing Ropes 3. Discussion 4. Literature ....		Abstract: In this project I want to analyse the break behavior of different famous knots. With stretch tests I figured out the load, at which a used climbing rope breaks. The experiments were not made with different new climbing ropes. So these tests here should only give a rough indication of stability in practical use.
		Max Bigelmayr, Okt. 2014

1. Mechanical Strenght of Knots in the Literature

Every rope has got a certain strength which depends on the used knots at the endings. In Climbing Rope Stretch and Fall Tests I analyzed the viscoelastic behavior of climbing ropes. At the endings of the rope I used Figure 8 knots to fix the rope. It is well known that the strenght of a knot (Knotenfestigkeit) is different for individual knots. But it´s not easy to get official informations about the stability of knots. Rope manufactors like Mammut, Edelrid, Beal, Tendon etc. did tests in their laboratories to determine the strenght difference of certain knots. Sometimes you may find some results of such tests in the Journals of Deutscher Alpenverein (DAV). In Wikipedia [1] you find the following table:

The data were collected 1999 by Edelrid with the static climbing rope „Everdry“ 11mm. I am not sure how many tests they did in their experiments and what´s the standart derivation of the data. So should one trust such data somewhere on the web?
I wanted to figure it out myself and tried to get a feeling of the strenghts of the Figure 8 knot campared to Bowline 1.5. Climbers often discuss dangers to use Bullin 1.5, because it could change the internal structure if you don´t care [2]. What about the strenght of the Bullin 1.5 knot, when you do it wrong? To find out the difference I made tests with the Bowline 1.5 when it´s made right or wrong. Mark Gommers did a great analysis of different types of Bowlines and explained how they are made [4]. He invented a special knot he called End Bound Single Bowline (EBSB) which seems to be the most stable knot known yet. Piotr Pieranski, Sandor Kasas, Giovanni Dietler, Jacques Dubochet and Andrzej Stasiak calculated and simulated the Breaking Process of Figure 8 knots [5]. They found out that breakage occurs at positions with high curvature at the entry to the knots. In special simulations they calculated the tights trajectories and curvatures of the overhand and figure-of-eight knot. In my experiments I want to find out the strenght difference of the Bowline 1.5, (wrong/right tied), Figure 8 knot and End Bound Single Bowline (EBSB).

2. Knot Strenght Tests with old Climbing Ropes

The experimental setup contains a 4 tone crane from Abus. A special strech setup with woodn beams and threaded rods was built:

Fig. 1a: climbing rope testing bench	Fig. 1b: climbing rope testing bench	Fig. 1c: 3000 kg crane scale	Fig. 1d: bottom hook with climbing rope

For a test a piece of climbing rope is cutted to a lenght around 3m. For statistical reasons I cutted up the old climbing rope into lenghts of 2,50m and sorted them to four bundles (1, 2, 3, 4) with the sequence 1, 2, 3, 4, 1, 2, 3, 4, 1, 2, 3,..... relating to the original rope. By this method the test samples of the knots are distributed well (f.e. the test ropes of figure 8 knots are the intervals [0m, 2.5m], [10m, 12.5m], [20m, 22.5m], [30m, 32.5m], [40m, 42.5m] from the original rope).

-Fig. 2a: Rope bundles	-Fig. 2b: Knot types for the tests.

On both ends the loops were tied with the knots I wanted to test. One loop of the rope will be thread into the hook of the beam on the floor (fig. 1d), the other loop will be thread into the hook of the weighing scale from steinberg systems (fig. 1c). The following films show tests of the Figure 8 Knot, Bowline 1.5 and Bowline 1.5 (wrong tied).

In general the rope breaks at positions which were part of the knot before. While stretching the ropes with the loop endings the knot shrinks tremendous before the break. While this shrinking process the rope is damaged by bending and friction [5]. Later these damaged rope parts are drawn out of the rope while stretching, so that the breaking point is some centimeters after the knot in the single rope area between the knots (Film 1-3).
The results of the experiments are summarized in fig. 3:

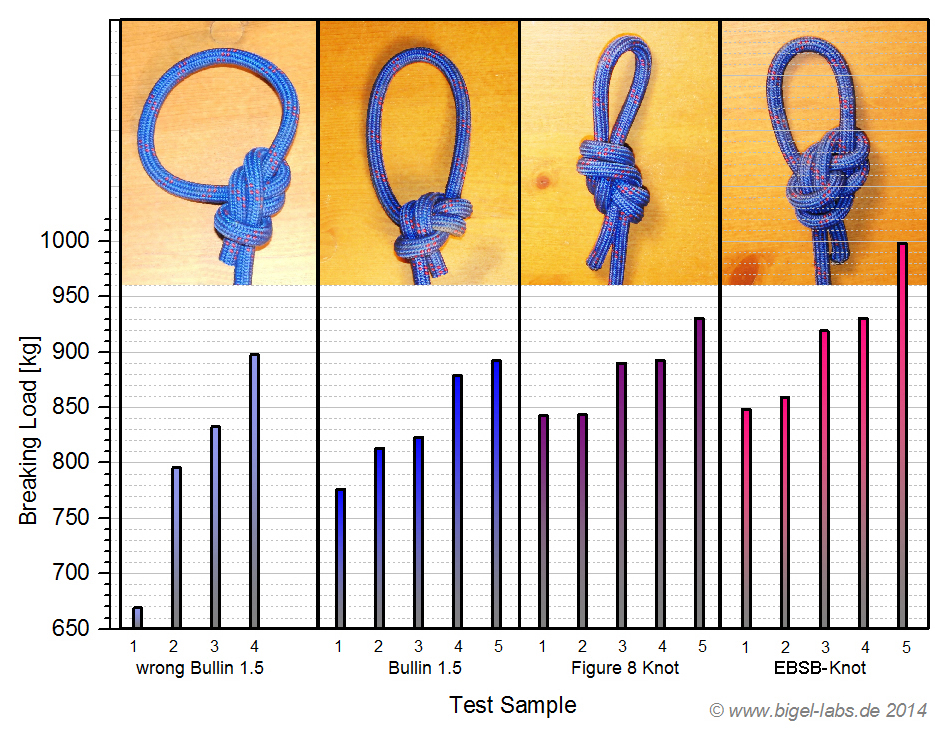
-Fig. 3: Experimental Measurements of Breaking loads for different knots with an old elastic climbing rope. The test samples are sorted by magnitude.

3. Discussion

Accordiong to fig. 3 the stability of the knots seems to grow up in the order Bowline 1.5 (wrong tied), Bowline 1.5, Figure 8 Knot, End Bound Single Bowline (EBSB). The deviation is in the order of appr. 90kg for each individual knot. So it does not make sense to do statistics with such little data. It´s obvious that the End Bound Single Bowline Knot is much moore stable compared to the other knots, as Mark Gommers predicated [4]. The data presented in fig. 3 give a real overview how the knots you may use do influence the stability of your system (rock climbing, raising of weights, rope swing..) when you use a old elastic climbing rope. I speculate that the standart deviation of the breaking load for individual knots is much less for new climbing ropes. Analysis of these influences could be the goal with larger sample numbers in future experiments.

4. Literature

[1] Knotenfestigkeit, Wikipedia, watched Okt. 2014
[2] Yosemite Bowline not safe for climbing, youtube film, watched Okt. 2014
[3] Figure 8 Knot, Wikipedia , watched Okt. 2014
[4] AN ANALYSIS OF BOWLINES, Mark Gommers, July 2013
[5] Localization of breakage points in knotted strings, Piotr Pieranski, Sandor Kasas, Giovanni Dietler, Jacques Dubochet, Andrzej Stasiak, New Journal of Physics 3 (2001) 10.1–10.13